Source: 📖 Problem Solving with Algorithms and Data Structures using Python ch7.15

What is an AVL tree?

An AVL tree is a type of binary search tree that always remains balanced in order to prevent important tree functions such as put and get from deteriorating to \(O(n)\) runtime, which would defeat the purpose of the tree. AVL stands for G.M. Adelson-Velskii and E.M. Landis, the names of its creators.

AVL trees maintain a balanced structure by keeping track of a balance factor – a number that represents how the nodes of the tree are distributed between the left and right sub-trees, calculated by the following formula:

$$balanceFactor = height(leftSubTree) - height(rightRubTree)$$

A balance factor of 0 indicates a well-balanced tree, where the left sub-tree and the right sub-tree are the same height. A positive balance factor indicates that the tree is biased to the left, while a negative balance factor indicates that the tree is biased to the right.

An acceptable balance range needs to be specified – a threshold value for the balance factor which, if breached, triggers a re-balancing of the tree to bring the balance factor back within the acceptable range. For this example, we will consider values between -1 and 1 (inclusive) to be balanced.

The following diagram shows the most unbalanced, but allowable, left-biased trees of heights 0, 1, 2, and 3, as specified by the above balance factor range:

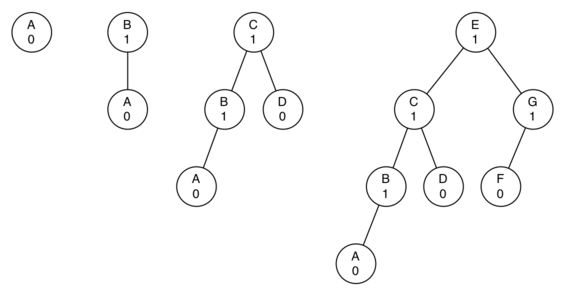
In each case, the tree has a balance factor of 1 as the left sub-tree is has one more height level than the right. If another node is added to the far-left of the tree in any of the examples above, it would breach the allowed range and the tree would need rebalancing, which we achieve through tree rotations.