Notes

< Back to previous note < Back to library

Source: 📖 Problem Solving with Algorithms and Data Structures using Python ch7.17

Rebalancing a tree with rotations

When an AVL tree's allowable balance factor range has been breached, a rebalancing must occur. The process by which a tree is rebalanced is called a rotation. When a tree is right-heavy, a left rotation must occur. When a tree is left-heavy, a right rotation must occur.

Here's an example of a left rotation on a right-heavy tree. The numbers inside each node represent its balance factor. Assume we are working with an allowable balance factor range between -1 and 1:

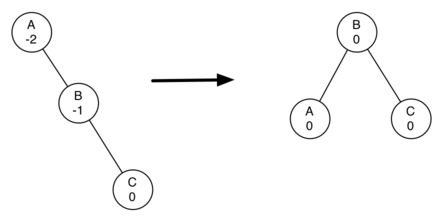
Right-heavy tree

The steps involved in a left rotation are as follows:

1. Make the right child (B) the new root.

2. Make the original root (A) the left child of the new root (B).

3. If the new root (B) already had a left child, make its left child the right child of the original root (A). We can guarantee that the original root's (A) right child slot is available, as it was previously pointing to the new root (B) but it no longer is as the new root is now its parent.

Below is a more complex example, this time dealing with a right rotation on a left-heavy tree:

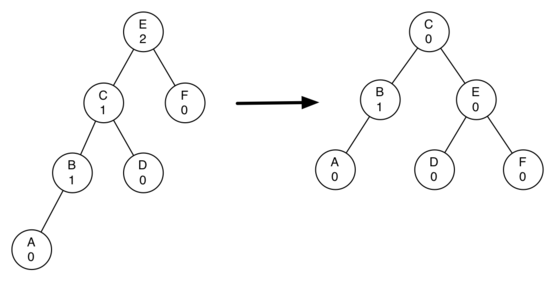
left-heavy tree rotation

The right rotation steps to rebalance this tree are as follows:

1. Make the left child (C) the new root.

2. Make the original root (E) the right child of the new root (C).

3. If the new root (C) already had a right child (D), make its right child the left child of the original root (E). We can guarantee that the original root's (E) left child slot is available, as it was previously pointing to the new root (C) but it no longer is as the new root is now its parent.

Notice that in both cases, rotation occurs around one particular node – the node whose balance factor exceeds the allowable range. In the first example, this was node A. In the second example, this was node E. Given that binary search trees (and therefore AVL trees) have a fractal structure, this node could be the root of the entire tree or the root of a sub-tree within a larger tree – the rebalancing process is completely agnostic to the node's position in the tree.