Source: 📖 Problem Solving with Algorithms and Data Structures using Python ch8.15

---

Implementing depth first search on a graph

A depth first search (DFS) algorithm has a main function, dfs, and a helper function dfs_visit which calls itself recursively on the vertices of a graph. We will implement both functions as methods of a Graph class, which will need some specific attributes to enable the functionality of the DFS algorithm. The Vertex objects that make up the graph will also need some specific attributes that the DFS algorithm utilises.

class Vertex:

	def __init__(self, key):
		self.key = key
		self.connected_to = {}
		self.distance = 0
		self.visited = False
		self.fully_searched = False
		self.predecessor = None
		self.discovered = None
		self.finished = None
	  
	def add_connection(self, to_vertex, weight=0):
		self.connected_to[to_vertex] = weight
	  
	def __str__(self):
		return str(self.id) + 'connected to: ' + str([vertex.key for vertex in self.connected_to])
	  
	def get_connections(self):
		return self.connected_to.keys()
	  
	def get_key(self):
		return self.key
	  
	def get_weight(self, to_vertex):
		return self.connected_to[to_vertex]
	  
	 
	class Graph:
	  
	def __init__(self):
		self.vertices = {}
		self.num_vertices = 0
		self.time = 0
	  
	def add_vertex(self, key):
		new_vertex = Vertex(key)
		self.vertices[key] = new_vertex
		self.num_vertices += 1
		return new_vertex
	  
	def get_vertex(self, key):
		if key in self.vertices:
			return self.vertices[key]
		else:
			return None
	
	def __contains__(self, key):
		return key in self.vertices
	  
	def add_edge(self, from_vertex, to_vertex, weight=0):
		if from_vertex not in self.vertices:
			self.add_vertex(from_vertex)
		if to_vertex not in self.vertices:
			self.add_vertex(to_vertex)
		self.vertices[from_vertex].add_connection(self.vertices[to_vertex], weight)
	  
	def get_vertices(self):
		return self.vertices.keys()
	  
	def __iter__(self):
		return iter(self.vertices.values())
	
	def bfs(self, start_vertex):
		start_vertex.distance = 0
		to_search = Queue()
		to_search.enqueue(start_vertex)
		while to_search.size > 0:
			current_vx = to_search.dequeue()
			for neighbour in current_vx.get_connections():
				if not neighbour.visited:
					neighbour.visited = True
					neighbour.distance = current_vx.distance + 1
					neighbour.predecessor = current_vx
					to_search.enqueue(neighbour)
			current_vx.fully_searched = True
	  
	def traverse(self, vertex):
		while vertex.predecessor is not None:
			print(vertex.key)
		vertex = vertex.predecessor
			print(vertex.key)

The Graph class has the DFS-specific attribute self.time. This is a simple counter that is incremented with each step the algorithm takes, which is then used by the individual Vertex objects to keep a temporal track of when the DFS algorithm visited them.

The DFS-specific attributes of the Vertex class are self.discovered and self.finished.

• self.discovered remembers the value of the Graph class' self.time attribute when the DFS algorithm first visits the Vertex object.
• self.finished remembers the value of the Graph class' self.time attribute when the DFS algorithm finished exploring the Vertex object.

With these attributes in place, we can now define the dfs and dfs_visit methods.

class Graph:

	[...]

	def dfs(self):
		for vertex in self:
			vertex.visited = False
			vertex.fully_searched = False
			vertex.predecessor = None
		for vertex in self:
			if not vertex.visited:
				self.dfs_visit(vertex)
	
	def dfs_visit(self, start_vertex):
		start_vertex.visited = True
		self.time += 1
		start_vertex.discovered = self.time
		for neighbour in start_vertex.get_connections():
			if not neighbour.visited:
				neighbour.predecessor = start_vertex
				self.dfs_visit(neighbour)
		start_vertex.fully_searched = True
		self.time += 1
		start_vertex.finished = self.time

The first line of the algorithm, for vertex in self, begins a loop of the values in the Graph object's self.vertices dictionary. These values are Vertex objects. Next we mark each vertex's visited and fully_searched attributes as False in case they were True from previous DFS/BFS calls, and also remove any predecessor pointers.

With all vertices reset, we can now begin the depth first traversal of the graph. We loop through each vertex in the graph once again, but this time we call the helper dfs_visit on each vertex if the algorithm has not visited it yet.

The dfs_visit recursive method is where the heavy lifting occurs. We begin by marking the vertex on which it is called as visited, then increment the Graph object's time attribute. Next we set the vertex's discovered attribute to the graph's current time, before starting a loop of the vertex's neighbouring vertices. Inside the loop, we first check if each neighbour has been visited. If it hasn't, we point its predecessor attribute to the current vertex, and recursively call dfs_visit on the neighbouring vertex. Since dfs reset all visited attributes earlier, all new nodes encountered will trigger a recursive call, meaning that the dfs_visit method will continually move through the graph to the first available neighbouring vertex until it encounters a vertex with only one neighbour, its predecessor, which has of course already been visited. At this point the loop through this 'dead end' vertex's neighbours ends as there are no more vertices to visit, and we mark the vertex as fully searched. Next we increment the time, and set the vertex's finished attribute to the graph's current time. The function call for this dead end vertex is now resolved and it is removed from the call stack, so the program returns to the for neighbour... loop in the previous call. If there were more neighbouring vertices to explore in the previous call, the for loop resumes to the next neighbour, otherwise the for loops end as it did with the dead end vertex, and the function call is resolved and removed from the call stack.

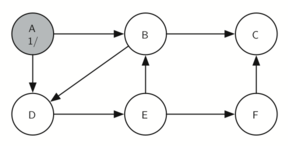
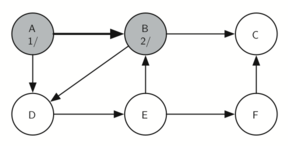
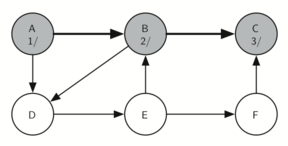
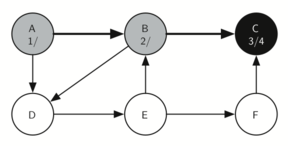
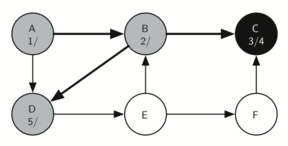
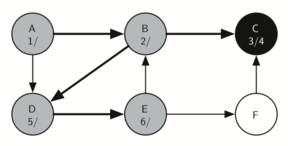
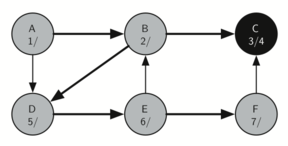
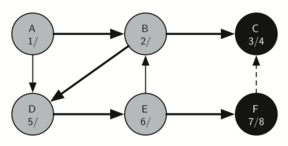
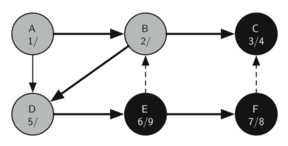
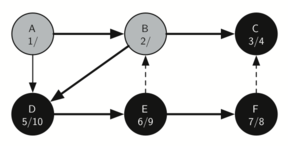
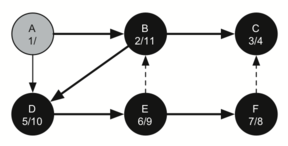
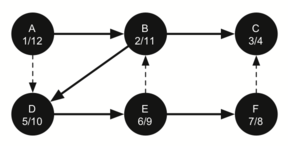
The following sequence of images demonstrates this process on a simple graph. Unseen vertices are coloured white, visited vertices are coloured grey, and fully searched vertices are coloured black. Underneath each vertex's name, the time each vertex was first visited (discovered) and fully searched (finished) are noted in the format vistied/finished. Edges that lead to nodes that have previously been visited (and therefore don't require further exploration) are represented by dotted arrows.