Source: 📖 Problem Solving with Algorithms and Data Structures using Python ch7.17

---

Implementing an AVL tree using python

An AVL tree inherits most of its properties and methods from a regular binary search tree but it updates some of them to implement its balancing functionality, and adds some methods of its own.

The first changes we will make to the regular binary search tree is to overwrite the _put method and write a new method, update_balance.

class AVLTree(BinarySearchTree):

	[...]

	def _put(self, key, value, current_node):
		if key < current_node.key:
			if current_node.has_left_child():
				self._put(key, value, current_node.left_child)
			else:
				current_node.left_child = TreeNode(key, value, parent=current_node)
				self.update_balance(current_node.left_child) # new line
		else:
			if current_node.has_right_child():
				self._put(key, value, current_node.right_child)
			else:
				current_node.right_child = TreeNode(key, value, parent=current_node)
				self.update_balance(current_node.right_child) # new line

def update_balance(self, node):
	if node.balance_factor > 1 or node.balance_factor < -1:
		self.rebalance(node) # rotation
		return
	if node.parent != None:
		if node.is_left_child():
			node.parent.balance_factor += 1
		elif node.is_right-child():
			node.parent.balance_factor -= 1
		if node.parent.balance_factor != 0:
			self.update_balance(node.parent)

New nodes added to a binary search tree (and AVL trees) are always leaf nodes. Because of this, a new node's balance factor is always 0. However, a new node will always change its parent's balance factor – if it's a left child, we must decrement the parent's balance factor by one; if it's a right child, we must increment the parent's balance factor by one.

There are also instances where a new node may affect the balance factor of ancestor nodes beyond its direct parent, even up to the root in some cases. For example, when a new leaf node extends a sub-tree to a new level that hadn't been reached anywhere else in the tree before this, all it's ancestor nodes' balance factors will have been affected.

Since updating the balance factor is a recursive function, we must define the base case. In this instance, there are two:

• The recursive call has reached the root of the tree.
• The balance factor of the parent node has been adjusted to 0.

Why does the balance factor of a node changing to 0 trigger a base case? When a node's balance factor is changed to 0, it means it has been brought into balance – its left and right sub-trees are now the same height. The only time a new leaf node can bring a sub-tree into balance is if the sub-tree's left and right branches had a height of \(x\) and \(x+1\), or vice-versa. When a new leaf node balances out this unevenness it hasn't extended the depth of the tree to a new level, therefore all ancestor nodes before the direct parent were already aware of the existing level that the new leaf node has become a part of.

class AVLTree(BinarySearchTree):

	[...]

	def rotate_left(self, orig_root):
	    new_root = orig_root.right_child
	    orig_root.right_child = new_root.left_child
	    if new_root.left_child != None:
	        new_root.left_child.parent = orig_root
	    new_root.parent = orig_root.parent
	    if orig_root.is_root():
	        self.root = new_root
	    else:
	        if orig_root.is_left_child():
	                orig_root.parent.left_child = new_root
	        else:
	            orig_root.parent.right_child = new_root
	    new_root.left_child = orig_root
	    orig_root.parent = new_root
	    orig_root.balance_factor = orig_root.balance_factor + 1 - min(new_root.balance_factor, 0)
	    new_root.balance_factor = new_root.balance_factor + 1 + max(orig_root.balance_factor, 0)

rotate_left is one of two tree rotation algorithms for rebalancing the tree when the allowable balance factor range is breached. Assume we want to rebalance the following tree, as node A has a balance factor of -2. Black arrows represent a node's child attributes and red arrows represent a node's parent attribute.

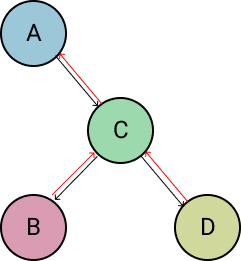
The first step is to set up a temporary variable to track the new root node (C), which we will call new_root. We then point the original root's (A) right child attribute to the new root's (C) left child with the line orig_root.right_child = new_root.left_child.

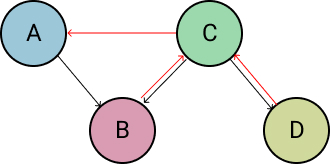
Next we check if the new root (C) has a left child. If it does, we point this left child's (B) parent attribute to the original root (A).

Next we point the new root's (C) parent attribute to the original root's (A) parent with new_root.parent = orig_root.parent. Note that this could be None if the original root was the root node of the entire tree.

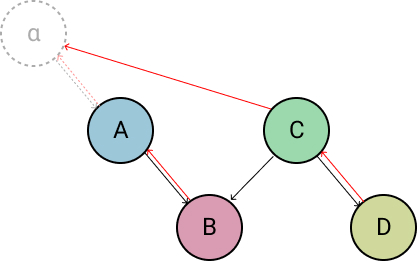
Next we check if the old root (A) was the root of the entire tree. If so, we change the AVL Tree's self.root attribute to point to the new root (C) instead. If it wasn't the root of the entire tree, it means that it must be either the left child or the right child of another node (α) and we must point that node's appropriate child attribute to the new root (C) instead of the original root (A). The code block responsible for doing this is:

if orig_root.is_left_child():
	orig_root.parent.left_child = new_root
else:
	orig_root.parent.right_child = new_root

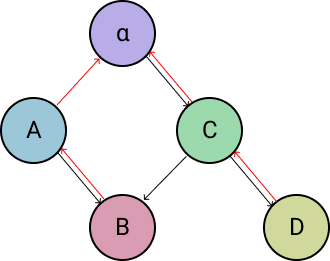
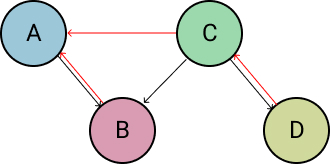
Next, we point the new root's (C) left child attribute to the original root (A) with new_root.left_child = orig_root and point the original root's (A) parent attribute to the new root (C) with orig_root.parent = new_root.

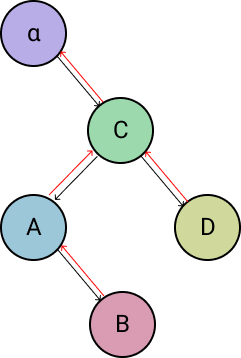
With this final change made, the binary search tree properties have been fully restored and we must now recalculate the balance factor for the original root (A) and the new root (C). The lines responsible for doing so are:

orig_root.balance_factor = orig_root.balance_factor + 1 - min(new_root.balance_factor, 0)
	    new_root.balance_factor = new_root.balance_factor + 1 + max(orig_root.balance_factor, 0)

The reason the balance factor for only these two nodes needs to be updated is because all other moves we made have moved entire sub-trees without changing their structure (and therefore without changing their balance factors).

Consider the following complete left rotation:

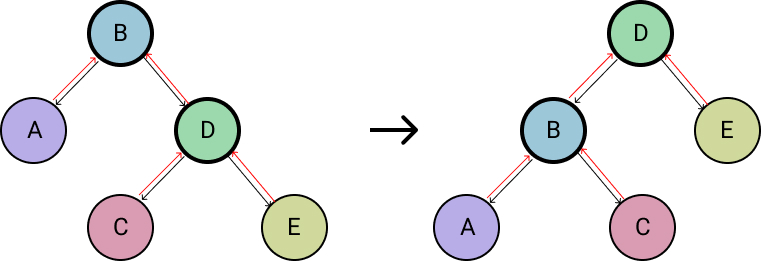
Nodes B and D are the pivotal nodes, while nodes A, C and E are their sub-trees. These sub-trees have not changed during the rotation process, their children (and therefore their heights) remain the same. We will use \(h_x\) to denote the height of a sub-tree rooted at node \(x\). With that in mind, we can assuredly say the following:

$$newBal(B) = h_A - h_C$$

$$oldBal(B) = h_A - h_D$$

We can also say with certainty that the old height of sub-tree D can be given by \(1 + max(h_C, h_E)\) – the height of D is the same as the height of its tallest sub-tree plus one. Combining this with the knowledge that node D's sub-trees have remain unchanged, we can derive the following:

$$oldBal(B) = h_A - (1 + max(h_C, h_E))$$

We can then subtract the old balance from the new balance and simplify the equation along the way using some algebra:

$$newBal(B) - oldBal(B) = h_A - h_C - (h_A - (1 + max(h_C, h_E)))$$

$$newBal(B) - oldBal(B) = h_A - h_C - h_A + (1 + max(h_C, h_E))$$

$$newBal(B) - oldBal(B) = h_A - h_A + 1 + max(h_C, h_E) - h_C$$

$$newBal(B) - oldBal(B) = 1 + max(h_C, h_E) - h_C$$

Next we can move \(oldBal(B)\) to the right side of the equation.

$$newBal(B) = oldBal(B) + 1 + max(h_C, h_E) - h_C$$

We can now utilise the following law:

$$max(a,b) - c = max(a-c, b-c)$$

For example:

$$max(4,5) - 3 = max(4-3, 5-3)$$

This law enables us to express the equation like so:

$$newBal(B) = oldBal(B) + 1 + max(h_C - h_C, h_E - h_C)$$

Which simplifies to:

$$newBal(B) = oldBal(B) + 1 + max(0, h_E - h_C)$$

Notice that we now have the expression \(h_E - h_C\) in the equation – this is the same as \(-oldBal(D)\) – that is, the negative of \(oldBal(D) = h_C - h_E\).

$$newBal(B) = oldBal(B) + 1 + max(0, -oldBal(D))$$

We can use another law in this instance:

$$max(-a, -b) = -min(a,b)$$

That is, the maximum of two negative terms is the same as the negative minimum of the same two positive terms. For example:

$$max(-3, -4) = -min(3, 4)$$

We can utilise this law to express our equation as the following:

$$newBal(B) = oldBal(B) + 1 -min(0, oldBal(D))$$

With this derivation in place, we can now consider how it relates to our algorithm. Node \(B\) is referred to by orig_root, while node \(D\) is referred to by new_root. It's now clear to see how the following line of code gives us the new balance factor for orig_root:

orig_root.balance_factor = orig_root.balance_factor + 1 - min(new_root.balance_factor, 0)

Similar logic is followed in deriving the new balance factor for new_root (\(D\)) during the line:

new_root.balance_factor = new_root.balance_factor + 1 + max(orig_root.balance_factor, 0)

There is one final edge case that we need to handle before having a fully functioning tree rotation mechanism. Consider the following right-heavy tree:

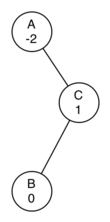
This tree requires a left rotation. However, when we apply a left rotation we end up with this tree:

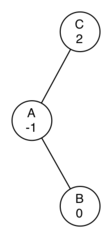
This tree now requires a right rotation, which would take us back to where we started. There are two symmetrical edge cases that we need to handle in order to fix this issue:

• When a sub-tree needs a left rotation to be rebalanced, first check the balance factor of the right child. If this right child is left-heavy, then a right rotation needs to be performed on the right child before proceeding with the original left rotation.
• When a sub-tree needs a right rotation to be rebalanced, first check the balance factor of the left child. If this left child is right-heavy, then a left rotation needs to be performed on the left child before proceeding with the original right rotation.

The following image shows what happens to our original tree when these steps are applied as necessary:

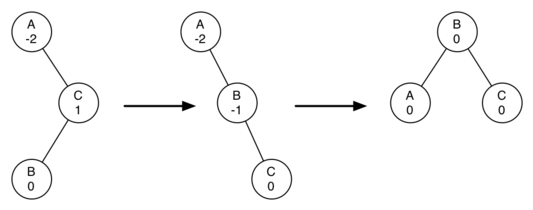
The method responsible for this process is called rebalance:

def rebalance(self, node):
	if node.balance_factor < 0:
		if node.right_child.balance_factor > 0:
			self.rotate_right(node.right_child)
			self.rotate_left(node)
		else:
			self.rotate_left(node)
	elif node.balance_factor > 0:
		if node.left_child.balance_factor < 0:
			self.rotate_left(node.left_child)
			self.rotate_right(node)
		else:
			self.rotate_right(node)